One often hears the argument that states with stricter gun laws have fewer firearm deaths. This is true, as the following plot of firearm death rates against the Gifford Law Center 1 ranking of states according to the strength of their gun laws shows2:
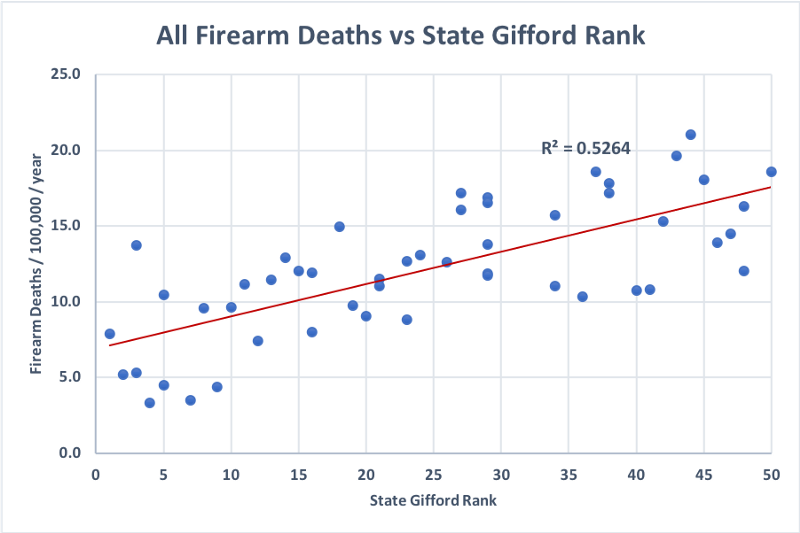
R²=0.5264 roughly means that differences in gun laws (as measured by the Gifford rank) “explains” 52.64% of the variation in firearm death rates between states. So certainly the strength (or weakness) of firearm laws correlates significantly with firearm death rates, as one might expect.
However, correlation does not imply causation, so let’s dig deeper. What happens if we just consider firearm homicides (i.e. leave aside suicides and other causes of firearm deaths)?

The predictive power of gun laws disappears completely for firearm homicides: only 1.19% of the variation between states is explained by differences in gun laws, and in fact that variation is not significant (t-stat of 0.77 for the statistically inclined).
What about suicides?
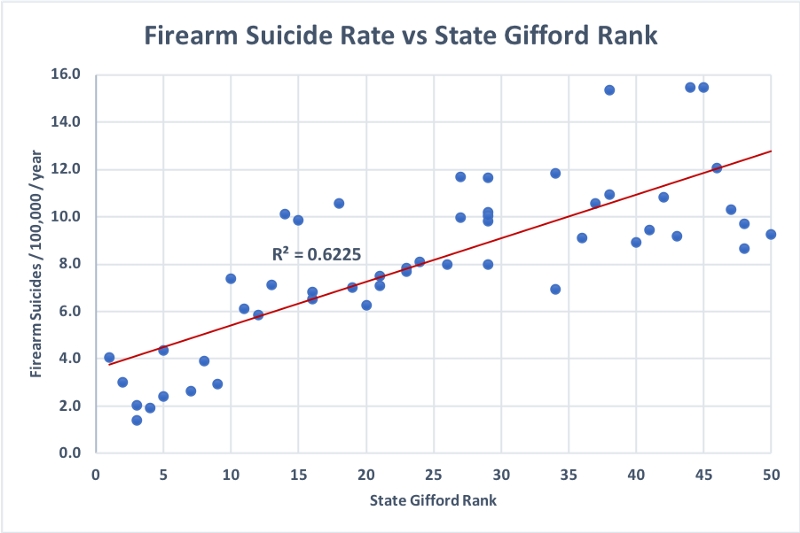
Here we see the origin of the predictive power of gun laws: stronger laws are correlated with fewer firearm suicides, with 62.25% of the variation in firearm suicide rates across states explained by differences in their gun laws. Later we will look into the predictive power of ownership and gun laws together — it turns out they are highly correlated, as one might expect. But first, let’s dig deeper into the homicides.
Explaining the Firearm Homicide Rate
If gun laws don’t explain the variation in firearm homicide rates between the states, what could? To answer this, take a look at the following chart showing the firearm homicide rate for the US, broken down by racial origin of the victim:
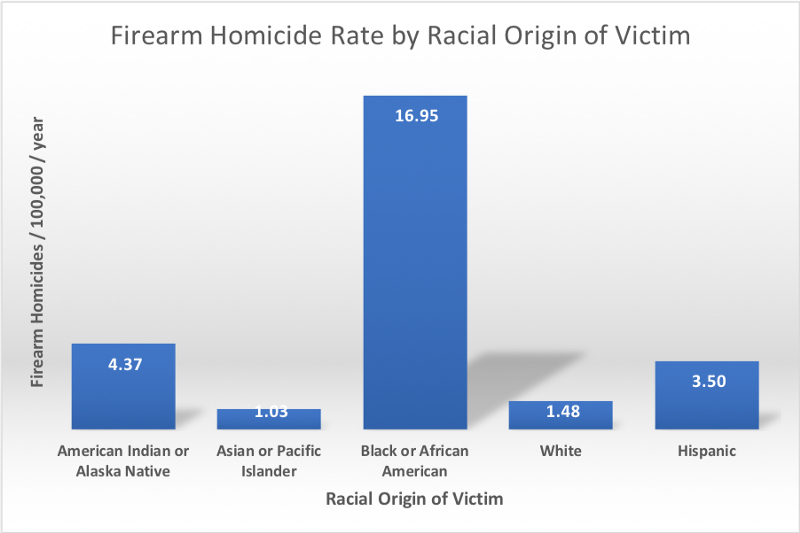
There is a large disparity between the firearm homicide rates for victims of differing racial origin. Since there is also a large variation in the racial makeup of the states, a reasonable initial hypothesis is that the variation in firearm homicide victim rates between the states might be explained in part by the differences in racial makeup of the states.
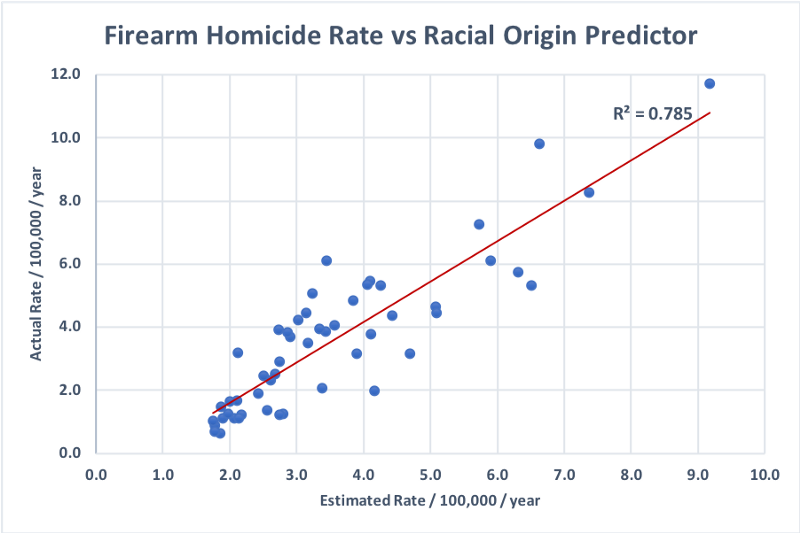
To test this hypothesis we construct a predictor of the firearm homicide rate for a state by multiplying the state’s population percentage of each racial group by the corresponding US-wide firearm homicide rate for the racial group, and summing them up. Call this the Racial Origin Predictor (ROP) (the linked spreadsheet has the details).
It turns out that almost all (78.5%) of the variation in firearm homicide rates between states is explained by racial origin:
Explaining the Firearm Suicide Rate
Firearm suicide rates also vary significantly by racial origin:
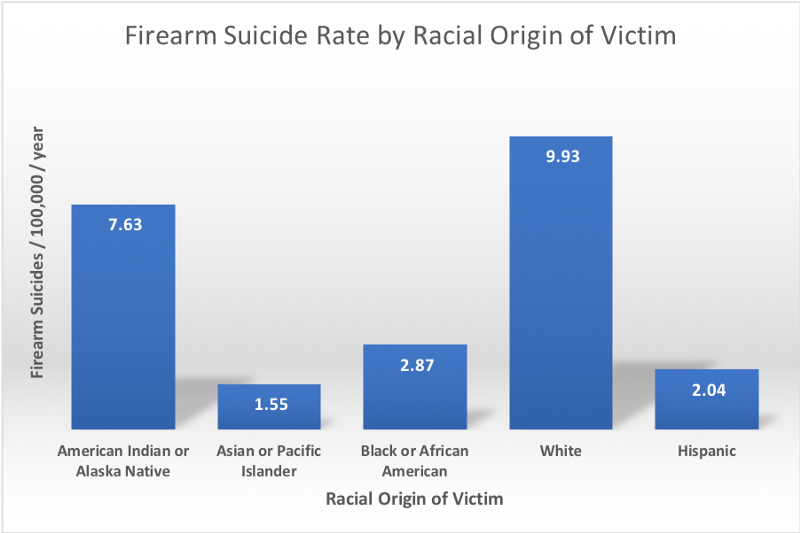
Given this variation, and the success of the Racial Origin Predictor (ROP) for firearm homicides, we might expect similar success for the ROP when predicting suicides. Surprisingly, this turns out not to be the case, with the ROP only accounting for 20.15% of the variation in firearm suicide rates between states, compared to 78.5% for firearm homicide rates.
Another candidate predictor is the firearm ownership rate, which turns out to be highly correlated to the Gifford Law Center rank (62.8%) and explains 54.06% of the variation in suicide rates between states.
The following chart shows the relative predictive power of various combinations of predictors (the chart shows adjusted R² which accounts for the fact that multiple predictors will always fit better than single predictors, even if the additional predictors have no explanatory power):

Although the Gifford rank and ownership are significantly correlated, they do appear to provide complementary information, as the predictor set with the most explanatory power is the combination of ROP, ownership, and Gifford rank, with an adjusted R² of 75%. We’ll call this predictor ROPOG.
Residual Analysis
Now that we have separate predictors for firearm homicide (ROP) and suicide (ROPOG) rates that each explain upwards of 75% of the variation between states, we can look at the outliers in the residuals to try and understand why some states outperform or underperform with respect to the predictor. The following map shows the residual ROP score (i.e. the difference between the ROP prediction and the actual firearm homicide rate in the state):
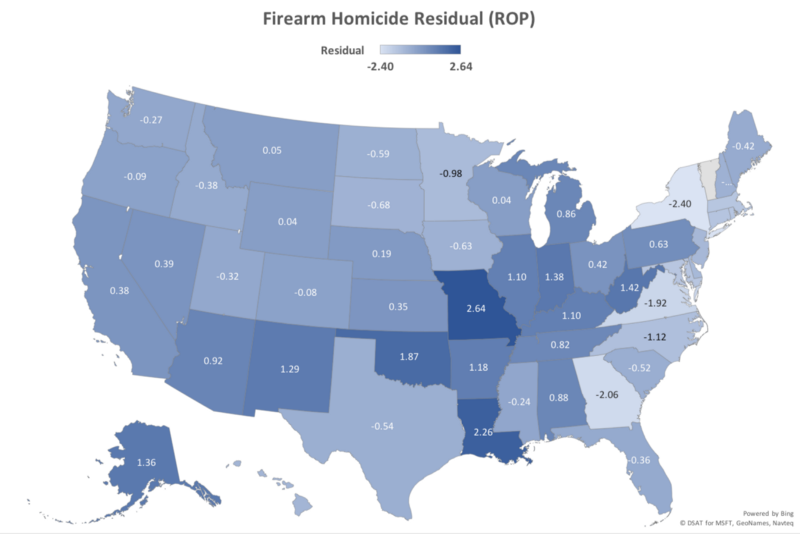
New York, Virginia and Georgia are the three most extreme negative outliers, with firearm homicide rates 2.40, 1.92, and 2.06 lower than the value predicted by ROP. Consistent with the lack of explanatory power of the Gifford rank for firearm homicide rates, while New York has a relatively low rank (i.e stricter gun laws) of 5, Virginia’s rank is 21 and Georgia’s is 29. It would be useful to understand what these latter two states are doing right, for whatever it is, it does not appear to be a function of their gun laws.
At the other end of the spectrum we have Missouri and Louisiana with firearm homicide rates 2.64 and 2.26 above their predicted values respectively. In this case gun laws may be part of the cause, as they rank 48th and 43rd respectively on the Gifford scale, and Missouri also has relatively low ownership of 27.1%.
Turning now to the the residuals for the firearm suicide rate predictor (ROPOG):
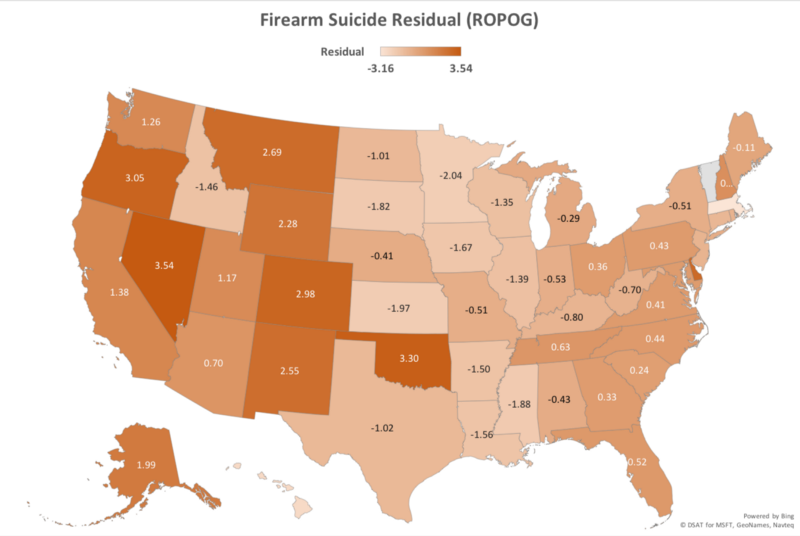
On the extreme lower-than-expected side we have Massachusetts (-3.16) and Hawaii (-2.62). Massachusetts is interesting because it is already low on ownership (22.6%) and strict on guns (Gifford rank 4), yet still manages to have far fewer firearm suicides than predicted. As with Virginia and Georgia, it would be useful to understand what Massachusetts may be doing right. Hawaii is reasonably strict on guns (Gifford rank 7), but has a lot of them (ownership of 45.1%), so one could be tempted to conclude that it is simply a very pleasant place to live.
There appears to be a significant geographical component associated with outlier states in terms of excess firearm suicides: they are overrepresented in the mountain states and west of the Rockies: Nevada (+3.54), Oklahoma (+3.30), Oregon (+3.05), Colorado (+2.98), Montana (+2.69), New Mexico (+2.55), Wyoming (+2.28). The only outlier state in the east of a similar magnitude is Delaware (+2.75).
- District of Columbia is not ranked by the Gifford Law Center — it was added manually to the data with a rank of 3 which appears consistent with their criteria. The results are not sensitive to its inclusion.
- The data and calculations used in this study are available here.